Introduction
This article is meant as an introduction to the basics of measuring position in both two dimensions and three-dimensions; specifically to the golf swing. I wrote it a while ago but would like to bring it back and then continue the idea.
Position Measurement in Two-Dimensions
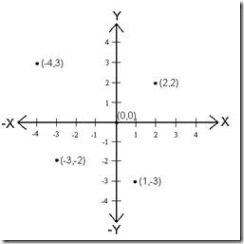
When we want to measure the position of something on a flat plane, say a piece of paper or the screen of a computer, we can use two perpendicular axes, one along the bottom and one along the left side of the paper. Lets give each of these lines a name, lets call the bottom one the X-axis and the one on the left side the Y-axis. These two lines join at the bottom left corner of the paper and we call this point the origin or (0, 0). It is zero feet along the X-axis and zero feet along the Y-axis. To place a point on the paper we can simply measure a specific distance along the X-axis and a specific distance along the Y-axis and write is as: (x, y). These two numbers completely define a point anywhere on our piece of paper. Now if we chose to move our two lines to the center of the page, that is, we draw a cross with one line up and down and the other left to right, we would now have added a negative X-axis and negative Y-axis. Anything to the left of the center will get a negative X value and anything below the center would get a negative Y value. Further, any point in the left bottom corner would have both X and Y values negative. The combination of the origin, the X-axis and the Y-axis is called a two-dimensional (2D) coordinate system or reference frame. The coordinate system below is labeled with several coordinate pairs as examples.
The Golf Mat as a Two-Dimensional Coordinate System
Now let’s take this piece of paper and lay it down on the floor, and let’s enlarge the paper to about a 5-foot square, paint it green and call it a golf mat coordinate system. If our golfer stood on this mat in the address position we could move the center (or origin) of our two lines between his feet. We can also make the line in the direction of the pin, red and call it the X-axis and make the line that is forward and backward with respect to the golfer, green (a different green than the mat so we can see it) and call it the Y-axis, maybe even position it through the ball for convenience.
Now since we have the golfer standing on a two-dimensional coordinate system we can measure certain things about his stance, for example, we can find the coordinates of the ball are (0, 3), that is, 0 feet along the X-axis and 3 feet along the Y-axis. We can also measure the positions of his right heel (0.8, 0), right toe (0.9, 0.8), left heel (-0.6, 0) and left toe (-0.7, 0.8). Note that all these values are in feet. Now we have some simple two-dimensional information about his stance. From these points we can calculate things like: width of stance, distance away from the ball, position of the ball between the feet, how much each foot is open or closed to the target in degrees, and if we draw a line connecting each heel we can calculate the angle that his stance is open or closed to the target. Note that the Y-coordinate of each heel is zero, which means he is square to the target in this example.
Measurement in Three-Dimensional Space
Now that we have the golf mat as our two-dimensional X-Y plane, lets add another axis and extend our discussion to the world we live in; three-dimensional space. Lets place an imaginary vertical line starting from the origin and going all the way to the ceiling. Lets color this line blue and call it the Z-axis. Now we have three axes, the X, Y and Z-axes and an origin. The origin is now defined with three number as (0, 0, 0), one each for its X, Y and Z values. The combination of the origin and the X, Y and Z-axes is called a three-dimensional (3D) global coordinate system or a global reference frame. We use the word “global” because it is the reference frame from which everything is measured. If we measure a distance along each of these three axes we can define any point in the 3D space around the golfer. Now we have the power to define the position of any point on the golfer’s body or club at the address position, not just the position of his feet and the ball as we did earlier.
Lets not worry how we do it for now but lets just assume we can measure the 3D coordinates of a point on his pelvis at the right thigh and at the left thigh. Lets also measure the position of a point on his left shoulder and a point on his right shoulder. Now we can join the left and right pelvis points with an imaginary line and the left and right shoulder points an imaginary line. From these lines we can measure some more interesting things about his stance. With the pelvis line we can measure whether his hips are open or closed at address, we call this the pelvis rotation angle, and how he is tilted to the right or left, we call this pelvis side bend. We can do the same for his upper body using the line from the left to the right shoulder. Notice that we can get rotation and side bend from this line but we cannot get forward-backward bend. We don’t know how much he is bending forward with his upper body since we only have a line from left shoulder to right shoulder. We need another line or point to figure that out. In fact we need to define a three-dimensional “local reference frame” in his upper body and all the other body parts in order to calculate everything we need for a true 3D analysis. I will explain this in my next article and also explain the term “six-degrees-of-freedom”. Here’s a hint; with a local reference frame on each body segment we can measure three positions - sway, thrust and lift (x, y, z) and three angles, one around each of the axes - forward bend, side bend and axial rotation (θx, θy, θz). Remember, positions are measured in feet (or meters) and angles are measured in degrees.